Журнальный клуб Интелрос » Философия науки » №1, 1995
(к вопросу о типе рациональности античной и декартовской геометрий)
Обсуждая проблему типологии рациональности, важно с самого начала развести понятия разумного в широком смысле слова и собственно рационального. Рациональное, рациональность не случайно тяготеют к научному знанию. Разумное в широком смысле слова охватывает более широкую культурную сферу. «Сказал безумец в сердце своем «Нет Бога»», – говорит 52 псалом Давида (Библия). Не-разумие (безумие) неверующего – эта оценка сразу определяет для нас то специфическое понимание разумности, внутри которой говорит псалом. Разумность здесь немыслима без веры, которая является необходимым условием ее. Говорить же о «рациональности веры» довольно трудно (и если возможно, то в очень специальном смысле). Разумность также бывает разная (как и рациональность) и определяется, в конце концов, тем образом истины, который является для данного воззрения характеристическим. Понятие же рационального выражает более узкий, специфический аспект истинного. Рационализация начинается тогда, когда начинается рефлексия о знании (и познании), когда желающее удостовериться в своей логической и философской вменяемости сознания хочет дать себе отчет о смысле собственной деятельности, о началах собственной конституции. Этот рефлективный характер рационального совсем не обязательное условие истинного и разумного в широком смысле слова. Отождествление разумного в широком смысле слова и рационального связано в нашей цивилизации (последних четырех веков) с определенным приматом рационалистической философии и отнюдь не является само собой разумеющейся истиной. Именно от Декарта идет традиция понимания познания как методического поиска знания, удовлетворяющего специфическим требованиям «ясности» и «отчетливости». Другие эпохи, другие культурные традиции совсем не делали такого акцента на самосознании, какой характерен для новоевропейской мысли. «И дивились Его учению, ибо Он учил их, как власть имеющий, а не как книжники» (Мф., 1,22), – характеризует Евангелие особую «методологию» проповеди Иисуса Христа. Не аргументы книжников, а особый спиритуальный аспект слова – может быть, более всего доступный сегодняшнему секулярному сознанию в поэзии, – свидетельствующий о некоей онтологической авторитетности говорящего – «учил их, как власть имеющий», – выступает здесь решающим аргументом в пользу истинности учения. Любая религиозно ориентированная традиция разделяет с христианством понимание истины, как некой духовной инициации. Однако и философия как определенная культура ума дает немало свидетельств понимания разумности – причастности ума к истине – как своеобразного озарения, имеющего квазирелигиозный характер. Речь идет здесь не просто о субъективных духовных «переживаниях», а о самих онтологических корнях мысли. Непреходящим памятником подобного понимания является философия Плотина. Человеческая мысль, по Плотину, укоренена в объективной мысли Божественного ума, способна подниматься до нее: «Взирая на себя, она видит живые существа, и ее взгляд осуществляется, и это осуществление есть она сама: мыслящий и мысль составляют одно целое. Она видит всю себя через всю себя же целиком... Пока мы были в высшем мире в реальности Божественного ума, очевидность этого нас удовлетворяла, мы были чистой мыслью, мы собирали все сущее в одно и созерцали. Это был тот самый Ум, который сам себя мыслил и говорил о самом себе. Душа пребывала в покое и позволяла действовать уму. Но теперь, когда мы вновь спустились сюда, нам хотелось бы убедить свою душу, нам хотелось бы увидеть модель в ее изображении (Эннеады, V, 3,6,5)»[1]. Подобное понимание самосущей мысли устойчивая черта тысячелетней платоновской традиции (в античности). С ним же связано и особое понимание психологии (спиритуалогии) мыслительного процесса. Уже у Платона мы находим уподобления мысленного поиска деятельности пророков и поэтов (об этом см. ниже). Мысль выступает здесь как целостный духовный акт человеческого существа, а не как отвлеченное мышление гносеологического субъекта.
Подобное понимание разумного трудно вместить в узкие рамки некоторой рациональности. Мы как бы имеем следующую иерархию уровней истины:
1. Истина – как истинное бытие, как идеал истины, в той или иной степени отчетливо выраженный в данной культурной традиции.
2. Разумное – как идеал причастности ума истине, имеющий интуитивный, а не дискурсивно-логический характер.
3. Рациональность – как проекция разумного, истинного на «плоскость» логического мышления, нормативное, дисциплинирующее начало в деятельности разума.
Каждый низший уровень является выражением (отражением) более высокого. Характер отражения, его адекватность, полнота различны для различных культурных традиций и сами являются определяющими особенностями изучаемых образований. Особый интерес представляет для философского анализа изучение соотношения разумного и рационального (дихотомия: разум – рассудок). Тем самым в рамках нашей схемы рациональное, не исчерпывая всей сферы разумного, выступает обычно в паре с иррациональным. Иррациональное, в свою очередь, естественно разделяется на дорациональное (дологическое) и сверхрациональное. Под сверхрациональным здесь понимается не просто (не только) мистическое измерение духовной (умственной) жизни, но, конкретнее, те особенности научной и философской мысли, которые обусловлены специфической ценностной ориентацией. Вся эта особая сфера, входя в общий объем разумного для данной культуры, не помещается уже в рамках только рационального, но при этом существенно влияет на него.
Мы будем обсуждать здесь различные понимания геометрии в свете двух различных типов рациональности. В науке тип рациональности характеризуется прежде всего своей методологией (в широком смысле этого слова). Каждая конкретная более или менее долгоживущая научная традиция отличается своим специфическим пониманием норм и смысла собственной деятельности. Сюда входит специальное понимание смысла доказательства и архитектоники знания вообще, т.е. особый методологический статус начал знания – аксиом, постулатов, правил, выводов, а также в той или иной степени осознанная, в той или иной степени сформулированная цель знания. Трудности обсуждения проблемы рациональности, по нашему мнению, связаны с определенной двойственностью этого понятия. Одной стороной оно обращено к чисто логическому анализу эпистемологических стратегий и, может даже быть, до определенной степени формализовано. С другой – устойчивые типы рациональности всегда несут на себе, как родимое пятно, след того специфического типа разумности, в рамках которого они рождены и интенции которого они все время проводят. Рациональность оказывается типичным фактом культуры, таким же двойственным как системы права, художественные школы или колебания моды. Рациональность как совокупность познавательных установок определяется не только представлениями о сущем, не только направлена на изучение этого сущего, но и в значительной мере на культивирование его во вполне определенных направлениях. Познание определяется не только сущим, но и в огромной степени представлениями о должном. Изучая типологию рациональности, мы переходим, так сказать, от чисто количественного отношения к знанию – знаем или не знаем? Как много знаем? – к качественной оценке знания: В каком смысле знаем? Что значит: как? знания и для чего? Осознание типа рациональности, характерного для данной эпистемологической традиции, выявляет связь данной традиции с определенным идеалом истины, с определенными мировоззренческими ориентациями.
***
Организующая роль типов рациональности, как тех архитектонических принципов, которые определяют саму конструкцию знания, наглядно проявляется в истории научных дисциплин. Одни и те же области исследования, порой даже те же самые проблемы, дают начало различным теориям, в зависимости от того, «в свете» какой рациональности она рассматривается. Любопытным примером здесь является история открытия аналитической геометрии. Это характерное детище Нового времени уже с XVIII столетия не только стало главным инструментом геометрических исследований, но и оказало огромное влияние на понимание математики в целом. Характерен пафос создателей аналитической геометрии: они осознают свою новацию как «возвращение к корням», как реставрацию того, что было известно уже математике древности, и что... сохранялось втайне. Декарт пишет по этому поводу в «Правилах для руководства ума»: «И мне по крайней мере кажется, что какие-то следы этой истинной математики обнаруживаются еще у Паппа и Диофанта, которые жили пусть и не в самую раннюю эпоху, но все же за много веков до нашего времени. Я поверил бы тому, что ее впоследствии утаили с неким опасным коварством сами авторы; ведь подобно тому, что многие мастера делали, как стало известно, со своими изобретениями, авторы, возможно, опасались, что эта наука, поскольку она была самой легкой и простой, обесценилась бы, став общедоступной, и вместо нее предпочли показать нам как результаты своей науки, чтобы удивить нас, кое-какие бесплодные истины, остроумно доказанные на основании умозаключений, вместо того чтобы учить самой науке, которая не оставила бы никаких поводов для удивления»[2]. Здесь важна для нас не столько эта несколько юмористическая подозрительность по отношению к древним. Она отчасти связана с общей для XVI–XVII веков установкой на «разоблачение тайн» и обретение «эзотерического знания», отчасти же с личными особенностями Декарта. Здесь гораздо интереснее эта неудовлетворенность ученого-философа всей старой конституцией знания, когда отдельные несвязанные положения, хотя и «остроумно доказанные», воспринимаются как «бесплодные истины». Декарт хочет систематического знания. Мы вернемся подробнее к этому ниже.
Античная математика действительно стояла на пороге открытия аналитической геометрии. То, чем вдохновляются Виет, Декарт, Ферма в XVI–XVII веках восходит не только к Паппу (IV в.) и Диофанту (III в.), но, по мнению некоторых исследователей, еще ко времени Евдокса и Теэтета (IV в. до P.X.). Во всяком случае, в XIII книге «Начал» Евклида в добавлении к первым пяти предложениям мы находим комментарий[3], который определяет и показывает в работе два специальных методологических приема – анализ и синтез. Именно сознательно подчеркнутая методологическая тенденция, характеризующая эти дополнения, подталкивала Виета и Декарта к генерализации этого приема. Анализ и синтез определяются следующим образом: «Анализ есть взятие искомого как допустимого путем последовательного <вывода, приводящего> к чему-нибудь, признаваемому за истинное. Синтез же есть взятие допустимого, из которого путем последовательного <вывода, получается нечто>, признаваемое за истинное»[4]. Из примеров видно, что анализ представляет из себя процедуру (логического) связывания искомого, предполагаемого истинным, с каким-нибудь положением, истинность которого известна. Синтез же дает обратное логическое движение, исходя из известного, истинного получают истинность того, что требовалось доказать. Все пять первых положений XIII книги «проводятся» в комментарии через процедуру анализа и синтеза. Разберем, например, 2 положение: «Пусть прямая CD будет в квадратах в пять раз больше своего отрезка DA; положим, что удвоенная DA будет AB; я утверждаю, что AB разделена в крайнем и среднем отношении в точке C и большим отрезком будет AC, которая представляет остаток первоначальной прямой»[5].
![]()
D A C B
![]()
Рис.1.
Доказательство ведется путем приравнивания некоторых площадей (произведение двух отрезков интерпретируется как площадь построенного на них прямоугольника). Античность не знает нашей алгебраической символики, но рассуждение строго следует пути, который в сегодняшних обозначениях мы можем записать так:
Дано:
(1) CD2 = 5 ‧ DA2,
(2) AB = 2 ‧ DA.
Нужно доказать:
AB/AC = AC/BC.
Сначала идет анализ. То равенство, которое нужно доказать, предполагается верным. По другому (через площади) оно записывается так[6]:
(3) AB ‧ BC = AC2.
Из условия (2) получаем:
AB ‧ AC = 2 ‧ DA ‧ AC.
Складывая эти два равенства (точнее, объединяя соответствующие площади), получаем:
(4) AB2 = 2 ‧ DA ‧ AC + AC2.
Но условие (2) влечет за собой немедленно:
AB2 = 4 ‧ DA2.
Заменяя в (4) AB2 получаем:
4 ‧ DA2 = 2 с DA с AC + AC2.
Наконец, прибавляя DA2 к обеим частям последнего равенства, получаем:
5 ‧ DA2 = DA2 + 2 ‧ DA ‧ AC + AC2.
Так как DA + AC = DC, то из рассмотрения площадей квадратов на DC, DA, AC следует, что правая часть последнего равенства равна CD2. Получаем 5 ‧DA2=CD2, то есть то, что предполагалось верным. Задача анализа выполнена: требующее доказательства положение, пока рассматриваемое как гипотетическое, связано логической цепочкой с предположениями (с тем, что считается верным). Однако это, конечно, не доказывает гипотетического положения (но, впрочем, может обнаружить ложность гипотезы, если полученное следствие противоречит предпосылкам). Уже во времена Аристотеляпонимают, что из ложного положения можно получить и истинное. Анализ как бы нащупывает тропинку от гипотетического положения, лежащего в области вероятного, но еще недосказанного, к области достоверного. Задача состоит в том, чтобы пройти по этой логической тропинке в обратном направлении: от достоверного к тому, что нужно доказать. Это обычно и осуществляет синтез: если положения нашей «логической тропинки» обратимы, то есть не только последующее следует из предыдущего, но и наоборот, тогда можно обратить и всю в целом логическую цепь доказательств анализа и получить необходимое доказательство выдвинутой гипотезы. Что, как легко видеть, справедливо и для нашего примера.
В обсуждаемом нами комментарии поразительна осознанность и четкость методологической установки. Неудивительно, что у Паппа мы уже встречаем разделение анализа на два вида: «цететика» и «пористика» (от греческих слов ζητέω – искать, домогаться, стремиться и πορίζω – доставлять). «Цететикой» называется анализ, применяемый при доказательстве теории, «пористикой» – анализ, приспособленный для нахождения решения задач, т.е. геометрических построений[7]. Такое внимание к аналитическому методу было неслучайно. Дело в том, что его разработка связывалась с традицией платоновской философии. А некоторые авторы прямо приписывали изобретение аналитического метода в геометрииПлатону. Последняя точка зрения и по сегодняшний день остается спорной. С ней не соглашались такие авторитетные историки науки как Хит (Th. Heath) и Мильо (G.Milhaud). Однако мы также думаем, что платоновские эпистемологические построения «подталкивали» геометров к выделению особого методологического приема в геометрии – анализа (независимо от участия самого Платона в непосредственном математическом воплощении этой идеи). Конечно, рассуждения того типа, которыми пользуется геометрический анализ, уже употреблялись в древнегреческой математике еще до Платона. Таков, например, метод доказательства от противного. В нем также мы делаем некоторые предположения, а потом разворачиваем его необходимые следствия до тех пор, пока не получим положение, противоречащее чему-то общепринятому. Метод доказательства от противного является как бы частным случаем аналитического метода. Но использование последнего до Платона является случайным. В платоновских эпистемологических схемах внимание специально обращается на архитектонику всего корпуса знания, что не могло, по нашему мнению, не повлиять и на методологическую культуру геометрии.
Основным методом у Платона, на которое обычно ссылаются при доказательстве его приоритета в использовании аналитического метода, является тот знаменитый фрагмент из VI книги «Государства», где дается платоновское разделение типов знания (в соответствии с типами бытия) («Государство», 510–511). Вся область познаваемого делится на чувственно познаваемое и умопостигаемое. Сфера чувственно познаваемого делится на область образов – «тени, затем отражения в воде и в плотных, гладких и глянцевитых предметах»[8], – и на область «самих предметов» – «живые существа, все виды растений, а также все то, что изготовляется»[9]. Область умопостигаемого, в свою очередь, делится также на две, подобно сфере чувственно постигаемого. Это сначала сфера условного знания (куда входят и математические науки). Здесь мы познаем, исходя из некоторых предпосылок, как, например, в геометрии, все построения которой связаны с принятием некоторой системы аксиом (и постулатов). Сами эти аксиомы в геометрии не обсуждаются. Тем самым достоверность нашего знания не выше достоверности этих аксиом. Знание оказывается неполным (условным). Кроме того, отмечает здесь же Платон, геометры, пользуясь чертежами, доказывают свои положения отнюдь не о нарисованных (материальных) фигурах, а о тех их идеальных прообразах, материальным «отражением» которых они являются. Все это «приглашает» нас к познанию «самих предметов» идеального мира, которые расположены на высшем этаже умопостигаемого мира. Здесь разум достигает беспредпосылочного начала (ἀνυπόθετον) и полноты знания. «Достигнув его (беспредпосылочного начала – В.К.) и придерживаясь всего, с чем оно связано, он (разум – В.К.) приходит затем к заключению, вовсе не пользуясь ничем чувственным, но лишь самими идеями в их взаимном отношении, и его выводы относятся только к ним»[10]. Для достижения этой области умопостигаемого служит диалектическая способность. Если обычные науки (и математика прежде всего) представляют собой изучение следствий предпосылок, как бы движение «сверху вниз» относительно некой воображаемой эпистемологической шкалы, то благодаря диалектической способности мы «поднимаемся вверх», то есть исследуем обусловленность самих предпосылок и достигаем согласно Платонубеспредпосылочного, самодостоверного начала, индуцирующего достоверность во все нижние этажи эпистемологического здания. Это движение не «вниз», а «вверх» от предпосылок (аксиом) наук происходит, собственно, уже не в сфере науки (а в сфере философии). Эти два движения требуют, по Платону, двух различных способностей: διάνοια (рассудок) в области наук и νοῦς (разум) – в области самих идей. Аналитический же метод как бы переносит движение вверх и в сферу науки, т.е. представляет собой применение разума в сфере науки. Хотя в обсуждаемом месте «Государства» Платон занят в основном объяснением диалектической способности в философии, тем не менее возможность продолжения «движения вверх» и на область наук присутствует в диалоге. Так Главкон, собеседник Сократа, говорит: «...Ты хочешь установить, что бытие и все умопостигаемое при помощи диалектики можно созерцать яснее, чем то, что рассматривается с помощью только так называемых наук, которые исходят из предположений. Правда, и такие исследователи бывают вынуждены созерцать область умопостигаемого при помощи рассудка, а не посредством ощущений, но поскольку они просматривают ее на основании своих предположений, не восходя к первоначалу, то, по-твоему, они и не могут постигнуть ее умом, хотя она вполне умопостигаема, если постичь ее первоначало» (подчеркнуто мной – В.К.). По своей природе область наук также постижима разумом, то есть и в ней возможно то движение вверх – от следствий к предпосылкам, – которым характеризуется сфера идей. Это движение мысли как исследование гипотетического и проблематичного, исходя из – или, имея в виду – достоверного, доказанного (интерпретируемого как следствие), выступает в науке как метод анализа.
Метод анализа на первый взгляд кажется чисто рассудочным способом выведения из гипотезы положений, считаемых верными (например, в разобранном нами выше анализе 2 положения XIII книги «Начал»). В то же время диалектическое применение ума, о котором говорит Платон, существенно связано со способностью интуиции, более того, с интеллектуальной интуицией, поскольку речь идет о созерцании идей. Знаменитая платоновская теория анамнезиса – интерпретация априорного познания как воспоминания о том, что видела душа «умными очами» по ту сторону смерти, в ноуменальном мире – вдохновляется именно опытом интеллектуальных (и духовных) озарений, а никак не рассудочным, силлогистическим, дискурсивным разворачиванием цепей логических следствий. Не случайно в «Меноне» в преддверии сцены, в которой Сократ, иллюстрируя теорию анамнезиса, заставляет мальчика-раба «вспомнить» решение задачи об удвоении площади квадрата, речь идет о жрецах и «божественных поэтах». Платоновский анамнезис есть всегда неожиданное – хотя и предчувствуемое, и настойчиво взыскуемое, – обретение более глубокого видения, есть прозрение. Это доказывает почти любой диалог Платона (в том числе и «Менон»). Здесь все время испытываются гипотезы, то есть делаются предположения и выводятся из них следствия (причем абсурдность следствия фальсифицирует и гипотезу). Сократ, организуя эти майевтические диалоги, заставляет собеседников преодолеть предрассудки, ложные мнения, заставляет их умственно сосредоточиться, как бы «вглядеться» в темную глубину незнаемого и «родить» – в смысле заметить, опознать, вербально зафиксировать – истинное представление. Такова работа диалектической способности, связанная с особым напряжением ума и интуитивным схватыванием истины. Ἐπιστήμη – точное знание как бы ставится в один ряд с поэтическим вдохновением и пророчеством. Можно ли и в аналитическом методе, происхождении которого связывается с платоновской философией, обнаружить нечто подобное?
На первый взгляд, как мы уже сказали, нет. Действительно, чисто фактически все рассуждение (анализ положения XIII, 2) представляет собой преобразование равенства, даваемого гипотезой (3), в равенства из числа данных (1) согласно основным логическим аксиомам Евклида: «если к равным прибавляются равные, то и целые будут равны» (аксиома 2), «равные одному и тому же равны и между собой» (аксиома 1). На первый взгляд ни для каких озарений здесь места нет. Но это только на первый взгляд. Анализ прост в рассматриваемом примере потому, что доказываемое положение 2 действительно верно и его доказательство, т.е. необходимая логическая связь условия и заключения теоремы, уже найдено. Однако понятиеанализ включает в себя, собственно говоря, более широкое содержание. Она заключает в себе и сам поиск того, что нужно доказать (заключения теоремы) и поиск необходимой логической связи между условием и заключением. Если мы не имеем ни того, ни другого, тогда мы вынуждены выдвигать в качестве заключения некоторые пробные положения – гипотезы – и исследовать насколько они совместимы с данными условиями. Пробными будут и сами положения, и пути связи их с условиями. Мы будем решать то, что в сегодняшней науке называется обратной задачей. Точнее говоря, даже более сложную задачу. Обратной задачей обычно называется проблема определения исходных данных по выходным данным, при условии, что сама процедура получения выходных данных из исходных известна. Но в общем случае анализа неизвестны и характер исходных данных («скрытые параметры»), и процедура, связывающая их с выходными данными. В этом случае мы можем действовать только «методом» проб и ошибок. То есть логически (и психологически) мы будем проделывать все то, что постоянно происходит в диалогах Платона: выдвижение и испытание гипотез. И то, и другое не подчиняется никаким фиксированным методическим правилам. И то, и другое для успешного завершения требует некоторого прозрения, «инсайта», интуиции (понимая последнюю одновременно и какугадывание, предвосхищение решения еще до его фактической реализации, и как некоторое действительное видение, то есть некоторое целостное, синтетическое восприятие условий, сторон проблемы, которое бы ясно представило роль изучаемых условий). Этот поиск решения очень трудно определить как следование какому-то правилу, методу. Скорее, большее значение играет опытность: в опыте выдвижения и испытания гипотез человек нащупывает подходы к истине, чтобы потом разом обрести некий новый интеллектуальный Gestalt, увидеть узловой, решающий пункт задачи. Здесь проявляется то, что называется собственно научным творчеством и что позволяло Платону сближать его строго научное знание – ἐπιυτήμη – с пророчеством и творчеством поэтическим. Авторитетный исследователь платоновской философии Ш.Мюгле писал о методе анализа: «Творческая спонтанность присутствует без малейшего ограничения уже в первой фазе нового метода, в этом первом интуитивном появлении геометрической истины, в той целостной реминисценции отношений, связывающих части фигуры, которую (реминисценцию – В.К.) никакой метод не смог бы породить и которая может быть нам дарована только благодаря θεὶα μοῖρα[11]. Аналитические процедуры могут быть преподаны и будут полезны каждому, кто обладает даром математической интуиции, но сам этот дар не приобретается»[12]. Греки отлично чувствовали этот момент, который всегда был известен математикам всех времен. Так великий Архимед при решении геометрических задач применял некий метод, использующий механические соображения. Метод не мог давать строгое доказательство: он использовал такие парадоксальные понятия как вес или центр тяжести какой-нибудь плоской фигуры[13]. Однако для Архимеда он имеет смысл лишь как эвристический метод, позволяющий ближе подойти к искомой формуле и угадать ее. Доказательство же этой уже наличной формулы можно потом сделать и легальными логическими средствами. В письме к Эратосфену Архимед пишет о своем методе: «Я уверен, что этот метод будет тебе ничуть не менее полезен и для доказательства самих теорем. Действительно, кое-что из того, что ранее было мною усмотрено при помощи механики, позднее было также доказано и геометрически, так как рассмотрение при помощи этого метода еще не является доказательством; однако получить при помощи этого метода некоторое предварительное представление об исследуемом, а затем найти и само доказательство, гораздо удобнее, чем производить изыскания ничего не зная. Поэтому и относительно тех теорем о конусе и пирамиде, для которых Евдокс первый нашел доказательство, а именно, что всякий конус составляет третью часть цилиндра, а пирамида – третью часть призмы с тем же самым основанием и равной высотой, немалую долю заслуги я уделю и Демокриту, который первый высказал это положение относительно упомянутых фигур, хотя и без доказательства»[14] (подчеркнуто мной – В.К.). Само угадывание формулы имеет также научную ценность (и есть факт научного обихода): наличная формула позволяет сосредоточить усилия в должном направлении (и доказать ее). Но подчеркнем, еще раз: обретение этой формулы есть факт скорее таинственный и чудесный (и поэтому в особенности он ценен!), не сводимый ни к какой методологии. В частности и метод, предлагаемый Архимедом, есть лишь эвристический метод, он лишь подводит к нахождению формулы, но отнюдь не отменяет того целостного духовного акта личности, благодаря которому лишь и свершается то, что называется открытием.
Античная геометрия, сформулировавшая для себя особые методологические процедуры – метод анализа и синтеза, стояла уже на пороге аналитической геометрии. Однако стояние это продолжалось почти 800 лет. Подобная задержка не бывает случайной. Как неслучайным было и то, что античная математика, открыв существование несоизмеримых отрезков, так и не сформулировала понятия иррационального числа. Для математики древности в этих открытиях не было никакого «порога», как преддверия здания новой теории. Вектор научного развития имел другое направление. В них была, скорее, граница науки, граница применимости ее понятий, граница рациональности. Ἄλογον – так и назывались иррациональные отношения. Чтобы продвинуться дальше, чтобы включить в науку и эти парадоксальные объекты, нужно было изменить сами нормы рациональности, сами критерии того, что считается понятным, а что нет. В случае иррациональности таким изменением было введение Евдоксом нового понимания отношений (точнее, равенства отношений), носящего откровенно позитивистский привкус. Метод же анализа, несмотря на то, что был осознан довольно рано, тем не менее не находил большого применения. Он оставался скорее школьным пропедевтическим методом, позволявшим лучше осознать логический «вес» решения. Метод анализа отнюдь не служил средством «открытия» формул. Античность очень хорошо понимала, что в том, что называется открытием, никак неустраним таинственный момент синтетического, целостного видения всей проблемы, носящий характер некоей дивинации (от лат. divinare – пророчествовать, предсказывать, предчувствовать). Продвигать науку (и методо-логию) туда, в эту таинственную сферу значило бы строить некую психо-логию творчества. Однако духовная чуткость, религиозная искушенность платоновско-пифагорейской традиции ориентировали ее на сознательное разделение в знании человечески-конструктивного от θεὶα μοῖρα, способов изложения от способов получения знания.
***
Чтобы осознать дистанцию, разделяющую декартовский подход к геометрии от соответствующего подхода античной науки, полезно вспомнить как вообще осознается в античности познавательный статус геометрии[15]. Пифагорейски-платоновская традиция понимает геометрию как науку двойственную, обязанную своим существованием двум принципам: интеллекту (разуму) и воображению. Интеллект есть способность чистого понимания, не требующая никакого чувственного образа (νοησις). Воображение – способность более низкого гносеологического статуса, связанная с чувственно воспринимаемым миром. Воображение важно в геометрии не само по себе, оно оказывается «преддверием» интеллекта, как пишет в своих «Комментариях на первую книгу «Начал» Евклида» Прокл.[16]. Хотя в геометрии используется только низшая часть интеллекта (διάνοια), тем не менее, занимаясь геометрией, человеческий ум должен восходить от познания, связанного с чувственностью мира образов, к познанию высших идеальных начал – «царства идей», в соответствии с онтологией Платона служащих прообразами всего сущего в мире материальном. Прокл пишет, что геометр «должен превратить изучение своей науки из самоцели в дело собственного пробуждения, перехода от воображения к чистому разуму, абстрагируясь в этом действии от протяженности и деятельности пассивного интеллекта, через что он увидит все вещи лишенными размеров и неделимыми, а именно: круг, его диаметр, многоугольники в круге, все вещи во всех и каждую отдельно»[17]. Увидеть вещи «лишенными размеров», «все вещи во всех и каждую отдельно» и означает, что речь идет не о чувственном (воображении), а об «умном» созерцании (θεωρία). С этой же двойственностью геометрии связано и разделение ее положений на теоремы и задачи. «Теоремы, – пишет Прокл, – превосходят задачи достоинством. Вся геометрия, поскольку она связана со многими ремеслами, кажется оперирующей на манер задач; однако, продвигаясь на манер теорем, она поднимается от задач к теоремам, от вещей второстепенных к первичным, от вещей, которые относятся скорее к ремеслам, к вещам, которые относятся к науке, в той степени, в которой эта наука имеет черты первой науки»[18]. Теоремы оказываются выше своим достоинством, так как говорят о вечных истинах, в отличие от задач, связанных с миром эмпирии. В деятельности διάνοια (рассудка) сказывается всегда его причастность высшей интеллектуальной способности. Это приводит к наличию неустранимой интуитивной компоненты в геометрических построениях, связанной не с воображением – следом низшей способности чувственного восприятия – интуиции чувственной, а с интеллектуальным созерцанием. Хотя треугольник и сложен из отдельных отрезков прямых, его свойства не дедуцируются из свойств прямой, как таковой. Идея треугольника также неделима, как неделимы слоги в известном рассуждении Платона из «Теэтата»[19]. Здание геометрической науки не поддается чисто рассудочному конструированию – «от общего к частному», – ее фундаментальные положения не складываются из частей, а требуют интуитивного постижения, «теорийного» созерцания. Этот акцент на интуиции отнюдь не означает, что геометрические теоремы не нуждаются в доказательстве. Однако роль доказательства – второстепенна. Математик не конструирует теоретического факта, не изобретает его, а обретает. Возможны различные доказательства одного и того же математического положения. Важны не они, а сам теоретический факт, предлагаемый созерцанию. «Божественный ум» видит истину этого факта непосредственно. Доказательства суть лишь необходимые для погруженного в чувственное, в становление человеческого ума «тропинки» к вечной истине, сами по себе случайные[20].
С этим же подчеркиванием интуитивного, созерцательного характера геометрии связано и внимание к эстетическим характеристикам геометрических объектов. «Все теоремы, – пишет Прокл, – познание которых не открывает доступ к большому числу других и которые не доставляют собой некоторого чувства элегантности и приятности, также оказываются вне области фундаментальных теорем»[21]. Наука согласно мышлению греков имеет не только «начала», но и цель. Так «Начала» Евклида разворачивают последовательность геометрических положений не с целью произвести их как можно больше, а с целью обеспечить построение (в XIII книге) теории правильных многогранников – геометрической основы платоновской космологии. Платон в «Тимее» так говорит о правильных многогранниках: «... мы никому не уступили бы в том, что нет видимых тел более прекрасных, чем эти, и притом каждое из них прекрасно в своем роде...»[22]. Аналогичных взглядов держится и Аристотель: «... заблуждаются те, кто утверждает, что математика ничего не говорит о прекрасном и благом. На самом же деле она говорит прежде всего о нем и выявляет его. Ведь если она не называет его по имени, а выявляет его свойства и соотношения, то это не значит, что она не говорит о нем. А важнейшие виды прекрасного – это слаженность, соразмерность и определенность, математика больше всего и выявляет именно их»[23]. Этот важный момент эстетического созерцания в геометрии связан с общими «теорийными» тенденциями античной геометрии, не сводимыми ни к чисто чувственному созерцанию, ни к голому рассудочному конструированию.
Здесь полезно вспомнить описание теории, «теорийного» видения в его исходном смысле греческого глагола θεωρεῖν (лат. contemplare), данное Г.Г.Гадамеромв статье «Похвала теории»[24]. Исходно слово θεωρία означает наблюдение, например, наблюдение звезд, или наблюдение зрителя за происходящим на театральной сцене, а также со-участие в некотором торжественном (религиозном) празднестве. Созерцание отнюдь не означает здесь просто смотрение как некое накопление информации о предлежащем. «Contemplatio пребывает не при некотором определенном сущем, но в некоторой области (Bereich). Theoria не есть, в своем главном, отдельное мгновенное действие, как некий способ, состояние, положение, в котором оказывается человек. Она (теория – В.К.) есть «бытие – присутствие» (Dabei-Sein), в том удивительном двойном смысле, который имеет в виду не только присутствие, но и то, что присутствующее есть «полностью присутствующее» («ganz dabei» ist). Таким образом есть участник какой-нибудь культовой процедуры или некоей церемонии, во время которой его внимание целиком поглощено этим соучастием, и этим предполагается, что это участие разделяют вместе с другими или возможными другими. Таким образом, прежде всего теория совсем не является тем способом, с помощью которого человек овладевает некоторым предметом или через объяснение делает его для себя достижимым»[25]. Для уяснения сверхпрагматического значения античного смысла «теории» Гадамер пользуется идущим от Августинаразличением смысла слова «иметь» в отношении двух родов блага. Один род блага характеризуется тем, что обладание им каким-нибудь индивидом исключает обладание другим (индивидом) тем же благом. Другой же род блага имеет ту особенность, что им, собственно, не может обладать никто и, в то же время именно поэтому каждый может быть ему причастен. Разница между ними описывалась Августином через разницу значений лат. глаголов uti – употреблять, применять и frui – наслаждаться. К первому, например, относятся все материальные блага. Ко второму роду Августин относил прежде всего созерцание Бога (молитва). Теория, по Гадамеру, есть именно причастность этому второму роду благ, в которой человек, отрешившись от всяких соображений полезности и выгоды, «чисто теоретически» относится к предмету своего созерцания (как, например, в чистой науке или искусстве). Гадамерподчеркивает в своей статье именно религиозные коннотации в греческом слове теория, характерно отличающие это понимание от новоевропейского, имеющего опору в самосознании. «Если мыслить значит созерцать, то здесь отсутствует какой-либо осмысленный вопрос о том, что могло бы быть предметом этого созерцания: оно есть как? себе самому открывающегося бытия, являющегося в том, что есть, что «для нас» представляется высшей степенью исполнения нашего «здесь» («Dа») – не некое «самосознание», но именно та интенсификация жизни, которую греки называли theoria и в незыблемом присутствии которой они признавали Божественное»[26].
«Начала» Евклида представляют собой удивительный памятник не только чисто математической мысли, но и свидетельство серьезной методологической проработки всего корпуса математики, ориентации науки на определенный идеал рациональности. Этим идеалом являлась традиция платоновской философии. Именно так воспринимались «Начала» математиками и философами античности. Прокл пишет: «Евклид был моложе учеников Платона, но старше Архимеда и Эратосфена..., придерживался платоновской системы и был адептом философии Платона. Именно в этом, между прочим, лежит причина того, что он представил построение платоновских фигур как результат своих «Начал»[27]. Свидетельства ориентации на платонизм при построении системы знания в «Началах» многообразны. Одним из таких характерных свидетельств является в «Началах» роль и логический статус движения. Движения применяются, например, при доказательстве равенства треугольников наложением (совмещением) (предложения 1,4; 1,8). Эти доказательства опираются на аксиому 7: «И совмещающиеся друг с другом равны между собой». В платоновской философии (во всяком случае в «Государстве») движение как принадлежащее сфере становления имеет более низкий онтологический статус. То же можно сказать и о его гносеологической роли: познание в терминах движения есть еще очень поверхностное познание, еще не достигшее точного знания, самого бытия. В VII книге «Государства» обсуждается эпистемологический «вес» геометрии. Главкон, собеседник Сократа, указывает на полезность знания геометрии в военном деле (и следовательно, на полезность этой дисциплины в деле воспитания истинного стража государства). Сократ соглашается, однако подчеркивает, что не в этом ее главное значение. «Надо, однако, рассмотреть преобладающую ее часть, имеющую более широкое применение: направлена ли она к нашей цели, помогает ли она нам созерцать идею блага? Да, помогает, отвечаем мы, душе человека обратиться к той области, в которой заключено величайшее блаженство бытия – а ведь это-то ей и должно увидеть любым способом.
– Ты прав.
– Значит, если геометрия заставляет созерцать бытие, она нам годится, если же становление – тогда нет.
– Действительно, мы так утверждаем.
– Но кто хоть немного знает толк в геометрии, не будет оспаривать, что наука эта полностью противоположна тем словесным выражениям, которые в ходу у занимающихся ею.
– То есть?
– Они выражаются как-то очень забавно и принужденно. Словно они заняты практическим делом и имеют в виду интересы этого дела, они употребляют выражения «построим» четырехугольник, «проведем» линию, «произведем наложение» и так далее: все это так и сыплется из их уст. А между тем все это наука, которой занимаются ради познания.
– Разумеется.
– Не оговорить ли нам еще вот что...
– А именно?
– Это наука, которой занимаются ради познания вечного бытия, а не того, что возникает и гибнет.
– Хорошая оговорка: действительно, геометрия – это познание вечного бытия.
– Значит, она влечет душу к истине и воздействует на философскую мысль, стремя ее ввысь, между тем как теперь она у нас низменна вопреки должному»[28](подчеркнуто мной – В.К.). Платон отмечает ту парадоксальность геометрии, что хотя она и использует движения, изучает она тем не менее вечное, и следовательно, неподвижное бытие, в котором нет места становлению. Движения, используемые в геометрии, должны служить обнаружению истин тождественного неподвижного бытия, «царства идей». Эта платоновски-пифагорейская точка зрения на познание, предполагающая неподвижность истинного бытия и соответствующие нормы познания (рациональность), в основном и проводится Евклидом в его «Началах». Движение здесь сведено к минимуму. Хотя и неустранимому. Последнее проявляется не только во введении аксиомы равенства, использующей движение (аксиома 7). Само разделение положений геометрии на теоремы и задачи, на факты, добываемые «умозрением», и факты, получаемые геометрическим построением – своеобразной формой «праксиса» (и требующей, следовательно, соответствующей праксиологии), – само это разделение, служащее ярким выражением платоновского дуализма между миром идей и миром становления, проходит сквозь все здание «Начал», вплоть до его самых первых элементов. Действительно, кроме определений Евклид вводит также два типа положений, которые являются собственно правилами вывода в его теории: постулаты (требования) и общие понятия (аксиомы). Аксиомы представляют собой общие положения, верные не только для геометрии, но и для других наук[29]: например, аксиома 1 – «равные одному и тому же равны и между собой». Постулаты же суть признанные возможности некоторых построений в геометрическом пространстве. Сама эта возможность, вообще говоря, проблематична, но геометрия принимает ее как некоторое допущение, для того чтобы построить более или менее богатую теорию. Интересно, как Аристотель определяет постулат во «Второй аналитике» (это определение цитирует в своем «Комментарии» и Прокл): «...Все то, что хотя и доказуемо, но сам (доказывающий) принимает не доказывая, если изучающему оно кажется правильным и он принимает его, есть предположение, притом предположение не вообще, а лишь для этого изучающего. Но если это принимают, в то время как изучающий не имеет никакого мнения об этом или имеет противоположное мнение, то постулируют это»[30]. Постулаты высказываются о возможном, о том, о чем часто изучающий «не имеет никакого мнения», о том, о чем возможны различные мнения (в отличии от аксиом, выражающих общепринятые представления). Через постулаты в теорию просачивается вся неопределенность, многозначность, связанная со сферой возможного. Ведь логические возможности этой области определяются не только сами по себе, но и тесно связаны с самоопределением человеческой свободы... Не случайно, что по поводу постулатов сразу возникает острая полемика: действительно ли возможно то, что они утверждают? Или в другой форме: не является ли возможность, утверждаемая постулатом, необходимым следствием других аксиом и постулатов, т.е. не является ли этот постулат теоремой или разрешимой задачей? Последний вопрос в отношении 5 постулата, как известно, выдвигался почти везде, где обучались по «Началам» Евклидаи где созревала более или менее высокая математическая культура. И в XIX веке было, наконец, установлено, что, действительно, возможны геометрии и без 5 постулата (или в его измененной форме).
Разделение правил вывода в геометрии Евклида на аксиомы и постулаты являлось, как мы уже заметили, как бы математическим отражением платоновского дуализма. Однако постулаты были лучшим выходом из положения, чем принятие движений. Разрешая движение в геометрии, мы апеллируем к воображению, к неопределенной и очень субъективной чувственной интуиции, что имеет чрезвычайно низкий эпистемологический статус в платоновской гносеологии. Постулат же, как бы «заключая в скобки» все субъективное, неопределенное, связанное с движением, формулирует возможностьиметь некий определенный результат и на основании этой возможности выводит дальнейшие следствия. Постулат представляет из себя род логического компромисса. В этом смысле интересен 4 постулат Евклида: «и что все прямые углы равны между собой». Прямой угол является естественным выделенным элементом во множестве всех углов. Именно по отношению к прямому углу определяются все другие типы углов. Поэтому утверждение о равенстве всех прямых углов необходимо для сравнения углов. Однако среди других постулатов четвертый выглядит довольно странно (как, впрочем, и пятый). Первые три постулата декларируют возможность построения прямой, проходящей через две точки, неограниченного продолжения любого отрезка и построения окружности произвольного радиуса с центром в произвольной точке. Четвертый же постулат утверждает равенство некоторого класса объектов. Но спрашивается: так ли уж было необходимо постулировать это равенство? Нельзя ли было его доказать? Тем более, что и само определение равенства фигур опирается на аксиому 7: «И совмещающиеся друг с другом равны между собой». Строго говоря, мы имеем здесь, в самых первых положениях «Начал» – аксиомах (общих понятиях) и постулатах – логическую несообразность. Если равенство определяется с помощью аксиомы 7, то 4 постулат необходимо должен быть теоремой. Иначе если мы произвольно приписываем какие-то конкретные отношения (равенство) каким-то фигурам, то естественно встает вопрос: не будет ли таким образом определенная геометрия противоречивой? Все это понимали уже геометры античности. Так Прокл в своем комментарии критикуетЕвклида за непоследовательность и дает доказательство 4 постулата методом наложения. В чем здесь дело? Нетрудно увидеть, что Евклид хотя и вводит аксиому 7, дающую возможность доказывать равенство фигур наложением, однако он стремится до минимума ограничить использование метода наложения. В первой книге из 49 положений наложение используется, собственно, только в двух: 4 и 8. Построения Евклида направляются вполне определенным идеалом рациональности – парменидовски-пифагорейски-платоновской оценкой движения как сущности, имеющей низкий эпистемологический статус, применения которой в строгой науке должно избегать путем редукции к каким-нибудь статическим формам доказательства. Действительно, метод наложения сразу ставит проблему: а сохраняются ли свойства фигур, передвигаемых в пространстве (для наложения)? Это трудный вопрос. Евклид не обсуждает его. Но введение 4 постулата преследует ту же характерную для последователя учения Платона цель: вопрос о свойствах движения «заключить в скобки», сформулировав отдельный постулат, имеющий дело только уже с результатом этого движения. Собственно, и первые три постулата «заключают в скобки» вопрос о движении. Строго говоря, они утверждают не то, что они говорят: можно «провести», «продолжить», «описать» (прямые, окружности). Они утверждают, в сущности, лишь следующее: при таких-то условиях считаем, что существует то-то. Они суть экзистенциальные, а не конструктивные суждения. Вполне в духе платоновского понимания знания геометрии Евклида хочет иметь дело с бытием, а не со становлением.
***
Заключая наше обсуждение того ориентированного на платоновско-пифагорейскую философскую традицию типа рациональности, который определял господствующее понимание геометрии в античности, мы отдельно сформулируем его характерные особенности:
1. Геометрия не является замкнутой в себе дисциплиной. Ее положение двойственно и двойственность эта обусловлена парадоксальностью ее задачи: чувственное явление интеллектуальных сущностей. В силу этого геометрия оказывается всегда открыта двум основополагающим бытийственным сферам платонизма – миру чувственности и миру идей. Но истина геометрии не в первом, а именно во втором. Геометрия выполняет задачу платоновского просвещения: помочь человеку преодолеть привязанность к чувственной сфере и обратить свой взор к миру истинного бытия, умопостигаемому миру идей. Более того, сама деятельность геометра невозможна без прозрений в этот высший мир, без озарений из этого мира. Эти озарения имеют характер целостного интуитивного акта, взыскуемого, но негарантированного и непредсказуемого дара и принципиально не поддаются никакой калькулирующей механизации.
2. Хотя актуально геометрия и представляет собой компромисс чувственной и интеллектуальной способности, тем не менее в ней статус «созерцательной составляющей» – теоремы, аксиомы – выше, чем статус «прагматических» методов – задачи на построение, постулаты. Знание в геометрии оказываетсяиерархичным. Эта иерархичность знания в геометрии (математике) отражает общую иерархичность платоновской эпистемологии (в соответствии с иерархичностью бытия в платонизме).
3. Нет чисто условного, формалистического подхода к математическому знанию. Хотя принятие постулатов и связывается с произвольными решениями (сравни вышеприведенную цитату из Аристотеля), тем не менее общая тенденция платоновской эпистемологии призывает к обсуждению обоснованности предпосылок, к преодолению их чисто субъективного смысла, к раскрытию их космологического значения. У античной математики нет вкуса к построению чисто формальной науки на базе произвольно выбранных предпосылок. Математика, как и другое знание, должна быть укоренена в самом бытии. Истинное знание – онтологично.
***
«Геометрия» Декарта как приложение к «Рассуждению о методе» выходит в 1637 году. Однако идея построения некоторого геометрического исчисления носится в воздухе уже в XVI веке. В 1591 году Франсуа Виет публикует свое сочинение «Введение в аналитическое искусство», в котором предлагает некоторую алгебраическую технику и применяет ее к геометрии. Этот свой метод решения геометрических задач Виет называет «цететикой» (следуя Паппу). Точнее говоря, цететикой называется и весь метод и его особая часть: «... Таким образом, имеется искусство цететики, благодаря которому находится уравнение или пропорция между искомой величиной и данными вещами; искусство пористики, с помощью которого на основании уравнения или пропорции изучается истина выдвинутой теоремы, и искусство эксегетики, благодаря которому из сконструированного уравнения или пропорции получаем саму искомую величину. И это полное тройственное аналитическое искусство может быть определено как наука отыскания истины в математике»[31]. Цететика, по Виету, основывается на силлогистике Аристотеля, однако непонятно как применять силлогизм, когда не ясно направление логического движения. С каждым силлогизмом связано обобщение, рассмотрение отдельной вещи как элемента некоторого класса. Вещь может принадлежать разным и разнородным классам одновременно, и в каком направлении строить силлогизм без дополнительной информации – совершенно непонятно. Это доверие к силлогизму идет от схоластической традиции. Мюглер справедливо писал в связи с этим, что, как правило, изобретатели новых методологий поддаются иллюзии универсальности их подхода: «Схоластическая философия считала, что в теории силлогизма она обладает ключом ко всем открытиям и Декарт также не был далек от мысли, что его великое изобретение, плод его гениальной интуиции, аналитическая геометрия избавляла геометров будущего от заботы быть также гениями»[32].
В духе этой же традиции универсальной науки (mathesis universalis) строит свое исчисление и Виет. Рассматриваемое сочинение заканчивается словами: «Окончательно, аналитическое искусство, представленное в тройственной форме цететики, пористики и эксегетики, по праву присваивает себе славу быть решением проблемы проблем, что значит нет неразрешимых задач»[33].
Этот своеобразный калькуляторский подход к науке – и к мысли вообще – довольно распространен в XVII веке. Может быть, наиболее рельефно он выступает у Т.Гоббса. Основным средством получения знаний является у автора «Основ философии» рассуждение (ratiocinatio). Однако в первом разделе своих «Основ», характерно озаглавленном «Исчисление или логика», рассуждение определяется следующим образом (глава 1 «О философии»): «Под рассуждением я подразумеваю, учитывая все сказанное, исчисление. Вычислять – значит находить сумму складываемых вещей или определить остаток при вычитании чего-либо из другого. Следовательно, рассуждать значит то же самое, что складывать и вычитать. ...Рассуждение, таким образом, сводится к двум умственным операциям – сложению и вычитанию»[34]. Далее следует объяснение на примерах. Так человек складывается из своих отдельных характеристик – тело, одушевленное, разумное. Совсем аналогично тому, как понятие квадрат получается в результате сложения представлений – четырехугольник, равносторонний, прямоугольный. Таким же образом отнятие отдельных представлений из некоторого их множества, характеризующего данную вещь, является, по Гоббсу, умственной операцией вычитания. «Не следует поэтому думать, – пишет английский философ, – будто операция исчисления в собственном смысле производится только над числами и будто человек отличается (как согласно свидетельству древних полагал Пифагор) от других живых существ только способностью считать. Нет, складывать и вычитать можно и величины, тела, движения, времена, степени, качества, действия, понятия, отношения, предложения и слова (в которых содержится всякого рода философия). Прибавляя или отнимая, то есть проводя вычисление, мы обозначаем это глаголом мыслить, что означает также исчислять, или умозаключать (logizomai)»[35]. Характерна чисто гносеологическая установка этого подхода: речь не идет здесь о реальности свойств вещей. Внимание сосредоточено на активности познающего субъекта, на операциях, совершаемых им. Эта особенность является общей чертой новой вызревающей к XVII веку эпистемологической традиции, нового типа рациональности.
Сущностью декартовской новации в геометрии являлась ее алгебраизация. Как действует метод Декарта в геометрии? Задача формализуется, т.е. ее величины выражаются буквами, последние связываются воедино некоторым уравнением, из которого и нужно найти неизвестную величину. Далее это уравнение преобразуется стандартными приемами, сводится к фиксированным простейшим и решается (с помощью геометрического построения). Главным, что обеспечивает эффективность, оказывается именно применение алгебры. Алгебра как таковая была известна в Европе еще задолго до Декарта. Ее использование в геометрии было освящено авторитетом арабских ученых (Аль-Хорезми, Омар Хайам и др.), осуществивших не только передачу для христианской Европы математического наследия, но и определенную транскрипцию его. Алгебра и выражала этот особый алгоритмический подход к геометрии (и к математике вообще). Работы Виета представляли алгебраические идеи уже достаточно созревшими, разве что лишенными еще удобных обозначений. Применение алгебры в геометрии не являлось открытием Декарта. Новым, что принесла с собою «картезианская геометрия», было принципиальное систематическое сведение геометрических задач к алгебраическим. Речь шла не о новых удачных приемах решения задач, а об изменении самой точки зрения на геометрию. Декарт подходит к геометрическим задачам с операционалистской точки зрения. Над числами можно производить арифметические действия, в числах можно считать. Геометрические отрезки также можно складывать и вычитать. Нельзя ли построить исчисление отрезков, подобное арифметическому исчислению? Тогда задачу на построение, задачу нахождения каких-то отрезков мы могли бы решать, следуя формальному алгоритму, аналогично тому, как это делается в арифметике. Действительно, для отрезков можно определить умножение и деление (и извлечение корня), и свойства этих операций будут подобны свойствам чисел. С этого и начинается «Геометрия» Декарта. Эти операции для отрезков были известны, конечно, еще грекам. И их подобие операциям над числами также было очевидно. Однако античная математика строго различает эпистемологический статус арифметики и геометрии. Первая наука занимается чисто интеллектуальными сущностями, из второй неустраним чувственный элемент. Эпистемологический статус арифметики выше, чем у геометрии. Декарт же уже движим другими познавательными идеалами, новым представлением о рациональности: «...к математике относятся лишь все те вещи, в которых исследуются какой-либо порядок или мера, и не важно, в числах ли, или фигурах, или звездах, или звуках, в любом ли другом предмете придется отыскивать такую меру; а потому должны существовать некая общая наука, которая, не будучи зависимой ни от какого частного предмета, объясняла бы все то, что может быть обнаружено в связи с порядком и мерой...»[36]. Декарт делает решительный шаг: он объединяет арифметику и геометрию в общую науку на основании операционального сходства их предметов. Это была общая наука, занимающаяся уже не числом и не протяженностью, а свойствами операций над ними, и называется алгеброй. При алгебраическом решении геометрической задачи собственно геометрический образ отходит на второй план. «Геометрия» Декарта занимается почти исключительно исчислением отрезков[37]. Находится соотношение, связывающее отрезки фигуры, получается уравнение, которое нужно решить, т.е. выделить из уравнения совокупность операций над известными отрезками для получения неизвестного. Так, если мы, к примеру, имеем квадратное уравнение
x2 + px – q = 0[38],
то его геометрический смысл, по Декарту, есть запись травиальности некоторой последовательности операций над отрезками.
Обозначим специальными символами следующие операции над отрезками:
S (y;z) означает сложение отрезков
y и z : (y + z).
Sub (y;z) – означает вычитание отрезков
y и z : (y – z),
m (y;z) – умножение (y ‧ z),
sq (y) – возведение в квадрат (y2),
sqr (y) – извлечение корня (√y),
d (y;z) – деление (y : z).
Тогда геометрический смысл квадратного уравнения есть выражение того факта, что после некоторой последовательности операций над известными и искомыми отрезками мы должны получить «0», т.е. отрезок нулевой длины:
sub (s (sq(x); m (p; x)); q) = 0.
Задача же «решения» этого уравнения превращается в следующую: используя данное соотношение между операциями и отрезками, а также некоторые тождественные соотношения, справедливые для операторов (например, sub (s(y;z);y) = z, т.е. (y + z) – y = z), выразить x как результат действия операторов на известные отрезки (т.е. p и q). Решение уравнения (имеющее геометрический смысл)
x = (√(p2 + 4q) – p)/2
через операторы записывается следующим образом:
x = d (sub (sqr (s (sq (p); 4q)); p); 2).
Этой формальной записью мы хотим подчеркнуть, что основное внимание в декартовском методе решения геометрических задач направлено на технику оперирования с отрезками. Характер геометрического знания здесь по сравнению с античным существенно трансформируется. Античность тоже решает задачи (строит с помощью циркуля и линейки, например), но античная геометрия немыслима без созерцания, причем, как мы подчеркивали, рассматривает познавательный статус теорем даже выше, чем задач. Античность созерцает, Декарт же вычисляет. Геометрическая интуиция – в обоих смыслах: и в смысле чувственного созерцания, воображения, и в смысле интеллектуального, как целостного видения, «схватывания» решения – оказывается как бы совсем ненужной. Тем более бессмысленно говорить здесь об эстетическом аспекте геометрии. Весь человек, во всей полноте своих умственных способностей уже как бы не нужен в аналитической геометрии. Рассудочный механизм нового метода может только считать согласно формальным правилам алгебраического исчисления. Радикальную реформу всей математики, которая была связана с алгебраизацией геометрии в «Геометрии» Декарта, известный историк математики Г.Цейтен справедливо сравнивал «с переходом индустрии от ремесленного к фабричному производству»[39].
Декарт не скрывал своих далеко идущих планов. Алгебраизация геометрии была только лишь математическим выражением его общего философского метода. Этот метод, собственно, должен был построить некую универсальную науку – mathesis universalis, – чисто формальным разворачиванием положений которой можно было бы получить все доступное человеку знание. Этот метод Декарт ищет на путях трансцендентализма. Вспомним рассуждения из «Правил для руководства ума». Философ начинает с соображения, что в основании всех наук лежит одна и та же тождественная себе человеческая мудрость, относящаяся к разным наукам, как солнце к различным освещаемым предметам[40]. Для познания, следовательно, было бы гораздо полезнее, чем искать «многознания» в науках, обратиться к исследованию законов самой этой мудрости. На этом пути Декарт формулирует основные положения своего метода. Принимать за истинное должно только ясное и достоверное. Для опознания этого достоверного служит способность интуиции[41]. Некоторые истины, сами по себе сразу не очевидные, могут быть связаны цепочкой умозаключений с исходными, самоочевидными, для чего и служит вторая основная способность-дедукция. Однако в разысканиях истины, настаивает Декарт, не должно радоваться любому, случайно открытому верному положению. Двигаться к истине должно методически; только это гарантирует нам фундаментальность получаемых результатов и их полноту. «Под методом же, – пишет Декарт, – я разумею точные и простые правила, строгое соблюдение которых всегда препятствует принятию ложного за истинное и без излишней траты умственных сил, но постепенно и непрерывно увеличивая знания, способствует тому, что ум достигает истинного познания всего, что ему доступно»[42] (подчеркнуто мной – В.К.). Строгое соблюдение «точных и простых» правил обеспечивает прогресс познания. Метод, однажды найденный, уже не требует для своей эксплуатации особых интеллектуальных усилий. Пользование им в науке сводит последнюю к своеобразной «механической работе», безличность которой, как неукоснительное, невозмутимое следование предписанным правилам, служит даже гарантом правильности получаемых результатов и, следовательно, их истинности. Эта общая наука, охватывающая все сферы, относящиеся к порядку и мере, должна иметь вид некоторого исчисления, mathesis universalis. Строго проведенный методизм с необходимостью превращается в калькуляторство.
Идея «всеобщей математики» (mathesis universalis) была в высшей степени популярной в Европе XVI–XVII веков. Источники этой идеи различны. С одной стороны, она выходит к тому образу математики, под которым она культивировалась в древних цивилизациях Египта, Вавилона, Индии. Здесь математическое знание выступает в основном не как совокупность теорем, а как набор определенных алгоритмов, позволяющих решать те или иные задачи. В арабской средневековой математике это понимание начинает обретать вид некоторого исчисления, прообраза нашей алгебры. Эта алгебраическая техника и манящий призрак «универсального алгоритма» достаются в наследство и Европе. Но и в античной науке были свои предпосылки универсальной «калькулирующей» науки. Аристотелевское понимание математического как абстрактного, как субъективное выделение специфических «общих» сторон вещей прокладывало дорогу формальному оперированию с математическими сущностями. Так во «Второй аналитике» мы читаем: «То же самое и (с положением о том), что члены соотношения переставляемы[43], будут ли они числа, линии, тела или отрезки времени. Подобно тому, как доказательство иногда могло бы вестись в отдельности, точно также можно дать одно доказательство всего; так как, однако, все они, а именно числа, длины, отрезки времени, тела, таковы, что нет какого-то единого (наименования) для них и они по виду различны между собой, то их брали каждое в отдельности. Теперь же (доказательство) касается того, что есть общее (в них), ибо (данное свойство) присуще не поскольку они линии и числа, а поскольку они обладают тем, что предполагается присущим как общее»[44]. Наконец, сама идея логического «Органона» как орудия (греч. ὄργανον – орудие, инструмент) для достижения истины также подводила к идее «универсального алгоритма». Этим постоянно соблазнялась средневековая схоластика[45].
Античная математика, глубоко осознавая роль аналитического метода при построении доказательств (например, у Паппа), тем не менее не пошла по путитехнизации геометрии, построения формального геометрического исчисления, по пути, который оказался магистральным для новоевропейской геометрии. Причина этого заключалась, как показано было выше, в самом понимании того, что есть геометрическое знание, что в свою очередь диктовало соответствующие нормы рациональности. Но геометрия, начиная с XVII века нарушает и другой характерный для античного типа рациональности принцип – принцип иерархичности знания. Мы подробно обсуждали выше принципиальное для платоновской методологии математики разделение на теоремы и задачи (построения) эпистемологический смысл того красноречивого факта, что, несмотря на необходимость введения движений в геометрию (в постулатах и даже в аксиоме), Евклид в «Началах» стремится свести использование движение до минимума. Декартовская геометрия совершает и в этом пункте революцию: происходит переоценка познавательного статуса движения. Оно не рассматривается больше как становление, нечто неоформленное, незаконченное и в силу этого неподлежащее познанию, направленному на незыблемое, неподвижное, на бытие. В начале второй книги своей «Геометрии» Декарт высказывает удивление, что геометры древности, позволив использовать построения циркулем и линейкой, с такой настойчивостью ополчались против более сложных «механистических» кривых. Ведь и циркуль и линейка тоже, строго говоря, представляют собой некоторые механизмы. Декарт же начинает употреблять для построения кривых уже более сложные механизмы, как, например, его «машина» для построения любого числа средних пропорциональных («мезолябий»)[46]. «Чтобы провести все кривые, которые я здесь намерен ввести, – пишет Декарт, – нужно только то предположение, что две или несколько линий можно перемещать вдоль друг друга и что их пересечения образуют другие линии; это предположение мне представляется ничуть не более трудным (чем допущенные античными геометрами движения – В.К.)...; но мне кажется совершенно ясным, что если – как это и делают – почитать геометрическим то, что определенно и точно, а механическим то, что не таково, и если рассматривать геометрию как науку, которая учит вообще познанию мер всех тел, то из нее так же мало следует исключить самые сложные, как и самые простые линии, если только можно представить себе, что эти линии описаны непрерывным движением или же несколькими такими последовательными движениями, из которых последующие вполне определяются им предшествующими, – ибо этим путем всегда можно точно узнать их меру»[47]. Декарт олицетворяет собой новую рациональность. Результаты древней математики хорошо известны в XVII веке, но заветы ее уже полностью забыты... Декарт просто не понимает почему с такой осторожностью относились к введению движений в геометрию античные математики[48]. Вся парменидовско-платоновская «подкладка» античной математики уже не находит отзвука в умственной совести новой культуры. Меняется сам идеал истины и меняется зависящая от него норма рациональности. XVII веку уже трудно согласиться с тем аргументом, что форма (идея) не складывается из частей, не получается «непрерывным движением». Что любое непрерывное движение, описывающее некоторую (геометрическую) фигуру, должно уже заранее «иметь» форму этой фигуры. И что, следовательно, форма эта предшествует всякой реализации, всякому построению. Декарт просто не понимает, что для античности введение движений в геометрию с помощью постулатов и аксиом представляет некоторый компромисс, некоторую уступку, противоречащую основным философски-методологическим принципам. XVII век слишком увлечен своей конструктивной деятельностью... И для этого направления мысли вопрос Декарта в высшей степени естественен: если какие-то «механические» движения допускаются в математике, то почему не допустить и другие, пусть более сложные? В чем критерий этой допустимости движений? – задает вопрос Декарт. И сам же отвечает на него своей конструкцией алгебраических кривых (т.е. кривых, уравнения которых выражаются многочленами). В геометрии, по Декарту, можно допускать все те кривые, для которых «можно точно узнать их меру». В чем же состоит эта мера кривой? – В формуле, задающей эту кривую, вот ответ Декарта. Формула описывает то постоянное соотношение, которое сохраняется между элементами кривой для любой точки кривой. Формула дает закон движения точки, описывающей кривую. Формула движения есть то «константное», статичное в движении, что определяет траекторию этого движения – кривую. Формула выражает закон порождения этой кривой и носит всегда конструктивный характер. Античная математика стремится в последнем счете к уяснению формы (идеи) геометрической фигуры, как некой целостной сущности, требующей для своего постижения соответственно и целостного же умственного акта – интеллектуального созерцания. Во всяком случае, в идеале такова цель занятий геометрией и такова же господствующая тенденция, методологический «вектор», направляющий геометрию. Вспомним еще раз характерное место из Прокла: геометр «должен превратить изучение своей науки из самоцели в дело собственного пробуждения, переходя от воображения к чистому разуму, абстрагируясь в этом действии от протяженности и деятельности пассивного интеллекта, через что он увидит все вещи лишенными размеров и неделимыми, а именно круг, его диаметр, многоугольники в круге, все вещи во всех и каждую отдельно»[49]. Алгебраизованная геометрия Декарта также по-своему «абстрагируется» от протяженности, заменяя изучение кривой изучением соответствующего ей уравнения, формулы кривой. Однако абстрагирование Прокла есть призыв к подъему разума на более высокую ступень в эпистемологической иерархии, призыв к «теорийному» зрению, таинственным образом преодолевающемугетерогенность пространственности и «видящему» «все вещи во всех и каждую в отдельности». Абстрагирование же Декарта есть построение формулы – рассудочной алгебраической схемы механического порождения кривой. Иерархичность знания больше уже не беспокоит математиков. Алгебраическое исчисление, справедливое равно для чисел и геометрических величин, описывающее как статические, так и кинематические конструкции, выступает однородным универсальным языком познания.
Э.Кассирер во введении к своей книге о Лейбнице дал прекрасное описание той существенной особенности в понимании познания, которая в главном определила пути новоевропейской науки. Ясность и отчетливость, которых требует от познания Декарт, оборачиваются на деле значительной теоретической «нагруженностью» любого научного вопрошания. «Каждая проблема познания, – пишет Кассирер, – содержит уже некоторую предпосылку, поскольку она – хотя бы для того, чтобы быть понятной самой себе – должна положить в основание определенные нормы (Gesetzlichkeit) познания»[50]. Эти же предвзятые нормы познания, определяющие вопрос, определяют и ответ: мы ищем определений предмета, подчиненных все тем же характеристическим нормам, которые были предпосылкой и вопроса. Познание, подвергнутое методической «муштре», просто не может воспринять неожиданного ответа: ответ должен всегда соответствовать смыслу вопроса. С этой точки зрения случайно полученные факты, вся голая эмпирия опыта не имеют никакого значения для науки. «Наука в строгом смысле дана только там, где сам предмет выведен из некоторого исходного единства метода»[51]. Именно поэтому внимание Декарта привлекает математика: она сама конструирует свой предмет. Поэтому и метод анализа приобретает для Декарта не только внутриматематический, но и общенаучный смысл. «...Анализ исходит из того, чтобы рассматривать искомое как данное. В условиях задачи он вскрывает средства ее решения. Он исходит при этом из основоположения, что каждая полностью определенная математическая проблема должна нести в себе условия своего решения. Каждый вопрос геометрии, к примеру, предполагает основные законы пространства; с другой стороны, каждый ответ, который ищет геометрия, не связан ни с какой другой реальностью, кроме как с закономерностью пространства. Проблема и решение, известное и неизвестное выступают здесь в том самом соотношении, которое принципиально требуется возможностью познания. Они принадлежат некоторой всеобщей систематической связи, которая однозначным образом реализуется в их взаимозависимости. В аналитическом методе неизвестное выступает как известное, поскольку оно определяется как раз через те предпосылки, которые лежат в задании; с другой стороны, известное выступает как неизвестное, потому что оно, в силу того, что его отношение к искомому еще не найдено, не определено систематически, в полной мере... Искомое в аналитическом методе имеет смысл не какой-то абсолютно независимой реальности, которая должна каким-то образом быть получена извне, но изначально рассматривается как определенное исходными предпосылками, из которых оно строго методически выводимо»[52]. Искомое конструируется из тех же самых элементов, которые лежат и в основе известного, данного, исходного. Всякая же данность, в свою очередь, должна быть редуцирована, должна быть разложена в совокупность этих элементов, допускаемых наукой (на это время) в качестве оснований. Тем самым методическое знание выступает как систематическая борьба со всякой данностью. Все, чем оперирует наука, должно быть сконструировано, должно быть методически выведено из некоторой совокупности элементарных, – то есть «ясно» и «отчетливо» познаваемых, – сущностей. Всякого рода качественные особенности редуцируемых сущностей должны быть элиминированы сведением к некоторому систематическому единству. Для математики то сближение числа и непрерывной геометрической величины, которое мы наблюдаем в алгебраическом методе Декарта, было только началом пути. Впереди было построение теории действительного числа и полное разложение пространства в «песок» теоретикомножественной модели Кантора...
Внимание методологии с наступлением Нового времени все более перемещается с тех сущностей, которыми оперирует наука, на те операции, которым подвергает ее субъект, на активность самого субъекта познания, что философски означает становление новоевропейского идеализма. Рациональность античной математики отражает платонистский идеал разумности вообще. Этот же идеал, правда, в его христианизированном варианте, направлял долгое время и средневековую математику. Человеческий разум, не вмещающий в себя всей актуальной бесконечности божественного познания, точнее, способный в науке лишь к потенциально бесконечному познанию, с неизбежностью воспринимает основные сущности, которыми оперирует познание (например, пространство, движение), как некую данность. Их последней причиной, скрывающейся в бездне непостижимого, выступает Демург, Бог – творец и его божественное: Fiat! – Да будет! С этой точки зрения и познание в своих основаниях выступает всегда как некий дар, как θεὶα μοῖρα. Соответствующую рациональность, ориентированную на осознание пред-заданных, до конца неразложимых сущностей, «форм» естественно назвать космологической рациональностью. Рациональность же Нового времени, направляемая пафосом конструктивного порождения, практически реализуется как развоплощение любой данности, любой предданной сущности. Эта рациональность отражает другой идеал разумности, обусловленный возрожденческим пониманием творения. Сущности, предстоящие человеческому познанию, сотворены Богом – инженером не однократным – и до конца неразложимым творческим «да будет!», – а эволюционным «разворачиванием» некоторых творческих принципов[53]. Человеческий разум, пантеистически причастный божественному, должен внутри самого себя найти эти творческие принципы, редуцировать всякую данность к ним и выразить в формуле закон построения этой данности. Эту рациональность естественно назвать антропоцентристской рациональностью.
***
Алгебраический метод Декарта в геометрии имел огромное влияние на математиков XVII века (и на всю последующую математику). Простота и эффективность метода (для некоторого класса задач!) обеспечили ему много защитников. Однако, реше2ния задач и доказательства, получаемые методом, существенно меняли саму «ментальность» геометрии. Например, нам нужно доказать теорему о биссектрисе внутреннего угла треугольника: Биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.
AM/MC = AB/BC
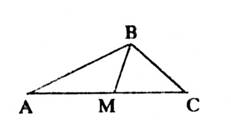
Обычно для доказательства теоремы делают дополнительное построение: продолжают AB, откладывают BD = BC, соединяют D с C. Тогда ∠ BDC = ∠ BCD (углы при основании равнобедренного треугольника), угол ∠ ABC равен сумме углов ∠ BDC и ∠ BCD (как внешний угол треугольника BDC).
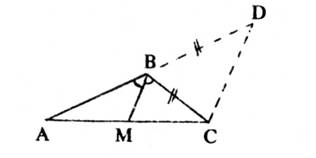
Рис. 3
Следовательно, ∠ MBC, половина ∠ ABC, равен∠ BDC. Значит, прямые DC и BM параллельны. Тогда из свойств параллельных прямых следует:
AB/BD = AM/MC
или, так как BD = BC
получаем
AB/BC = AM/MC
что и требовалось доказать. Понятно, что подобное доказательство невозможно получить с помощью метода аналитической геометрии.
Невозможно в том смысле, что метод не позволяет получать какие-то дополнительные построения: метод просто вычисляет. Обычный, то есть практиковавшийся с античности, «метод» в геометрии (в противовес методу аналитической геометрии его называют синтетическим) оставляет свободу инициативе новых подходов – проведению новых линий и усмотрению новых соотношений. Метод же Декарта скрывает все это богатство интуитивных возможностей за формализмом алгебраических уравнений. Чуткие умы почувствовали это уже в XVII веке. Великий Ньютон, прекрасно владевший алгебраическим методом в геометрии, не считал его тем не менее аутентичным выражением природы этой науки. «Уравнения, – писал Ньютон, – суть выражения арифметических вычислений, и они, собственно говоря, не имеют места в геометрии... Умножения, деления и тому подобные вычисления введены были в геометрию недавно и при этом неосторожно и в противоречии с основной целью этой науки. Всякий, кто рассмотрит построения задачи при помощи прямой и круга, найденные первыми геометрами, легко увидит, что геометрия была изобретена для того, чтобы мы, проводя линии, могли с удобством избегать утомительных вычислений. Поэтому не следует смешивать эти две науки. Древние столь тщательно отличали их друг от друга, что никогда не вводили в геометрию арифметические термины. Современные учения, смешивая обе науки, утратили простоту, в которой состоит все изящество геометрии. Арифметически проще то, что определяется при помощи более простых уравнений, геометрически же проще то, что определяется при помощи более простого проведения линий; и в геометрии следует считать лучшим то, что наиболее просто с геометрической точки зрения»[54]. Эта ньютоновская специфически геометрическая «простота» представляет собой апелляцию к особой оценочной способности, чувству естественности и изящества решения, способности, родственной художественному вкусу. Она воспитывается систематической работой с геометрическими объектами, служит не только оценочным, но и эвристическим средством в решении задач, и не поддается формализации. Выработать эту способность значит воспитать в себе ту «интуицию», о которой мы говорим, обсуждая античное понимание геометрии.
Метод аналитической геометрии стремится элиминировать всю эту интуитивную составляющую, свести решение задач только к калькуляции, быть средством, доступным самым посредственным способностям. Но действительно ли это ему удается? Оперирование с уравнением – приведение его к стандартным формам, решение его и геометрическая интерпретация – на самом деле представляет из себя лишь «запрограммированное «следование определенным правилам. Однако уравнение нужно сначала получить и составление этого уравнения отнюдь не поддается какой-либо определенной алгоритмизации. «Итак, – пишет Декарт в «Геометрии», – желая решить какую-нибудь задачу, следует сперва ее рассматривать как уже решенную и дать названия всем линиям, которые представляются необходимыми для ее построения, притом неизвестным так же, как и известным. Затем, не проводя никакого различия между этими известными и неизвестными линиями, нужно обозреть трудность, следуя тому порядку, который показывает наиболее естественным образом, как они взаимно зависят друг от друга, до тех пор, пока не будет найдено средство выразить одну и ту же величину двояким образом: это то, что называется уравнением, ибо члены, полученные одним из этих двух способов, равны членам, полученным другим»[55] (подчеркнуто мной – В.К.). Нужно найти «наиболее естественный» порядок зависимости элементов задачи (включая и искомые x) одних от других. Но как это сделать? Как оценить эту степень естественности? Как формализовать (алгоритмизировать) этот подход? Метод Декарта не дает ответа на эти вопросы. Составление уравнения остается «узким местом» всего декартовского подхода к геометрии[56]. Формальная алгебраическая калькуляция возможна лишь тогда, когда уже составлено уравнение. Однако его составление требует того целостного видения связи всех элементов задачи, которое не сводимо ни к какой формальной процедуре, которое приобретается только опытом. Составление уравнения у Декарта соответствует почти тождественно этапу античного анализа, т.е. связыванию логической цепочкой соотношения, которое пытаются доказать, с соотношениями, выражающими данные задачи. Этот этап, как мы уже говорили выше, требует некоторого интуитивного «прозрения», синтетического «схватывания» целостной системы элементов задачи, без которого, собственно, невозможно сделать ни шага к ее решению. В этом смысле декартовский метод делает все то же, что обычно осуществляет формализация в науке: он подчеркивает, выставляет на первый план то, что «понятно ему» (методу) – технику калькуляции с формальными символами. Все же остальное, что служит обеспечением этого метода, отодвигается за его границу, объявляется «преодоленным», субъективным, ненаучным. Однако чаще всего именно этот находящийся за границами метода «остаток» и оказывается самым органичным и неустранимым началом науки[57]. Доказательство К.Гёделем в 1931 г. знаменитых теорем о неполноте показало средствами математической логики иллюзорность надежды на универсальную формализацию математики, на сведение ее положений (и их доказательств) к работе чисто формального алгоритма. Первая теоремаГёделя о неполноте утверждает, что достаточно богатая, непротиворечивая формальная система (содержащая арифметику) неполна, т.е. содержит истинные положения, формализуемые в ее языке, которые недоказуемы и неопровержимы в терминах этой системы. Другими словами, для доказательства этих положений нужны иные средства, чем только лишь формально-логическое связывание высказываний. Неформальность процедуры составления уравнения в методе Декарта косвенно свидетельствует, по нашему мнению, о том же: в решении геометрических задач есть неустранимо «иррациональная», не сводимая к чистой калькуляции составляющая. Природа этой составляющей связана с принципиально «теорийной» (т.е. обусловленной созерцанием) природой геометрии, не поддающейся чисто методическому подходу.
Вместе с этим естественно встает вопрос о философской оправданности метода, методизма вообще и связанной с ними рациональности. Декарт дал не только описание своего метода, но и подробно рассмотрел все с ним связанное, все то «поле» методической «ментальности», непосредственным плодом которого этот метод является. Декарт настаивает, что познание невозможно, пока не будет познан сам орган познания. «Если кто-нибудь поставит своей задачей исследовать все истины, для познания которых достаточно человеческого разумения, – а это, мне кажется, надлежит сделать хотя бы раз в жизни всем, кто серьезно доискивается здравого смысла, – он наверняка обнаружит с помощью данных правил, что ничего невозможно познать прежде, чем разум, так как от него зависит познание всего остального, а не наоборот»[58]. Здесь, как известно, Декарт приводит пример, связанный с механическими ремеслами[59]. Человек, желающий заняться кузнечным делом и не имеющий готовых инструментов, должен будет сначала использовать любые подручные предметы – камни, полки, необработанное железо, – чтобы с помощью них «выковать» сначала необходимые инструменты – молотки, наковальню, щипцы и т.д. И только после этого с помощью этих специальных предметов – орудий труда – он может заняться собственно кузнечным делом: делать мечи, шлемы и т.д. Пример очень поучителен. Его аналог в философии – формулировка научного метода – характеризуется, действительно, тем же: движение мысли при формулировке метода неметодично. Оно не подчиняется тем критериям ясности и отчетливости, которые конститутивны для метода. Скорее оно носит характер некоторых интуитивных открытий, череды воплощений некоторого интуитивного принципа, предносящегося философу. Наш «становящийся кузнец» тоже пользуется подручными материалами при выделки орудий труда не согласно их «естественному» предназначению, а в плане определенной технологической перспективы: быть удобным для удара, быть гибким, тяжелым, огнестойким и т.д. Короче, соответствовать той цели, которая выдвинута человеком. Но откуда берется сама цель? Чем она оправдана? Декарт склоняется скорее к тому, что начала метода врождены нам. То есть человеческий разум носит в себе определенную тенденцию к подобным построениям (как если бы камни и палки существовали только для того, чтобы было создано орудие – молоток, топор и т.д.). Однако эта истина не исследуется методически. Она принимается как некий направляющий принцип некритически, мы вместе сДекартом должны «верить» в нее. Веря в нее, мы и в тех уже наличных научных дисциплинах («подручных предметах») – арифметике, геометрии древних – видим и используем только ту сторону, которая отвечает нашей «вере». При этом мы методически игнорируем другие стороны, мы культивируем не какую-то естественную, а вполне специальную форму рациональности. Эта форма рациональности связана с определенной антропологией, с представлениями о том, что и почему врождено человеку. Обсуждение последнего вопроса неотделимо от обсуждения ценностных, мировоззренческих ориентиров, скрытых в данной стратегии познания. Однако это должно быть предметом уже специального разговора.
Кассирер совершенно справедливо указывал, что правильно поставленный вопрос несет с собой уже достаточно много, а именно: он предполагает уже языксамого ответа. Вопрос задает направление в смысловой сфере; сосредоточившись именно в этом направлении, мы можем обрести и ответ. Однако в том и состоит вся трудность – как нужно задавать вопрос? В каком направлении? Декартовское вопрошание, вся эта «ясность» и «отчетливость» удивительно напоминает то вопрошание-допрос, которое достаточно известно нам в XX столетии по опыту тоталитарных бюрократий. Когда спрашивающий беспрерывно «уточняет» наши ответы замечаниями типа «говорите яснее», «отвечайте точно на вопрос», «не отклоняйтесь от темы», «вопросы задаю только я» и т.д., то в достаточно сложных случаях, – из которых, впрочем, состоит почти вся жизнь, – становится понятно, что через этот жесткий «методологический» раструб истина просочиться просто не может или же принимает в высшей степени искаженные формы. Истинный метод вопрошания должен удовлетворять взаимно противоречащим требованиям: он должен быть и достаточно определенным, чтобы поставить вопрос, но, с другой стороны, и достаточно «свободным», чтобы вместе с «грязной водой» несущественно не отфильтровать и «младенца» истинного. И вообще сомнительно, что подобное вопрошание можно организовать как некую формализованную процедуру. Момент дисциплинированности мышления, конечно, необходим истинному вопрошанию. Не случайно в «Меноне» Сократ и его диалогическое искусство сравниваются с морским электрическим скатом: у его собеседников «цепенеет душа и отнимается язык» после того, как логическая критика Сократапродемонстрировала им всю несостоятельность их, по видимости, таких очевидных, мнений[60]. Однако это не является самоцелью сократовских диалогов. Это оцепенение души и мысли, которое Сократ, по его признанию, испытывает и сам, есть лишь первый шаг к обретению умственной свободы, есть лишь симптом разрушения иллюзии обоснованности, застарелых предрассудков, без которого невозможна сама постановка вопроса. Только осознав свое незнание, можно двинуться вперед, можно сосредоточить умственный взор на непонятном и попытаться «схватить» ответ. Процедура эта, осуществляемая в диалоге, в высшей степени парадоксальна и таинственна, что и заставляет Сократа не раз сравнивать ее с мистериями[61]. Взятый же в своей отдельности метод – и методизм как идеология – всегда остаются сократовским «скатом», при всей самоуверенности своей рациональности грозящим мысли рассудочной оцепенелостью, заводящим ее в тупики и апории.
Примечания
[1] Цитата по книге: П.Адо. Плотин или простота взгляда. М., 1991. С. 44.
[2] Декарт Р. Соч.: В 2 т. Т. 1. М., 1989. С. 89.
[3] Во времена Виета этот комментарий довольно единодушно приписывался Теону Александрийскому (IV в.). Исследователь XIX столетия Гейберг (I.L.Heiberg) высказал предположение о принадлежности его Евдоксу (или Теэтету).
[4] Цитата из комментария Д.Д.Мордухай-Болтовского к книге: Начала Евклида. Книги XI–XV. M.;Л., 1950. С. 287–288.
[5] Цит. соч. С. 289. Напомним, что словами «АВ разделена в крайнем и среднем отношении в точке С» выражается справедливость равенства АВ/АС=АС/ВС.
[6] Евклида вместо этого равенства написано: «Прямоугольник между АВ, ВС будет равен квадрату на АС» (Цит. соч. С. 289).
[7] Pappus d'Alexandrie. La collection mathematique. Paris, 1933. P. 478.
[8] Платон. Государство. С. 510.
[9] Там же.
[10] Там же. С. 511.
[11] Греч. – божественный дар (удел).
[12] Mugler Ch. Plalon et la recherche mathematique de son epoque. Strasbourg-Zurich, 1948. P. 314.
[13] Парадоксальность состоит в том, что по самому определению плоскость имеет кулевую толщину и, вообще говоря, непонятно, как подобный объект мог бы иметь какой-то вес.
[14] Архимед. Послание к Эрастосфену. О механических проблемах. С. 299 // Архимед. Соч. М., 1962. С. 298–327.
[15] См. книгу: Катасонов В.Н. Метафизическая математика XVII века М., 1993. Гл. 1.
[16] Proclus de Lycie. Les commentaires sur le premiere livre des elements d'Euclide. Paris, 1948. P. 46.
[17] Op. cit. P. 47.
[18] Op. cit. P. 211.
[19] Платон. Теэтет. С. 205. 20
[20] Прокл пишет о разногласиях в Академии уже во времена Платона по поводу статуса геометрических положений. Одни (ученики Спевсиппа и Амфинома) считали, что все положения следует назвать теоремами, другие (ученики Менехма) – проблемами. Интересно, что Прокл считает правым и тех и других: «Без сомнения, справедливо, что о причинах, которые обнаруживаются в этих вещах (теоремах и проблемах – В.К.) и дают им форму, говорят как о вещах создаваемых; так как мы говорим, что стремление нашего рассудка и действие законов, врожденных ему, приводят к созданию фигур, существующих в воображении и к направлению на эти фигуры. Действительно, именно здесь [в воображении – В.К] происходит их образование; в то время как в рассудке все эти вещи присутствуют без какого-либо создания или изменения [подчеркнуто мной – В К.]. Геометрические построения представляют собой лишь разворачивание в пространстве и времени реальностей, извечно существующих в идеальном мире».
[21] Proclus... P. 65.
[22] Платон. Тимей. С. 53.
[23] Аристотель. Метафизика, 1078 а 34–40.
[24] Gadamer H.-G. Lob der Theorie. Reden und Aufsalze. Frankfurt am Mein, 1985. S. 26–50.
[25] Op cit. S. 44–45.
[26] Op. cit. S. 48–49.
[27] Proclus... P. 61–62.
[28] Платон. Государство. С. 526–527.
[29] Кроме специфически геометрических аксиом 7 и 9.
[30] Аристотель. Соч.: В 4 т. Т. 2. М., 1978. С. 275.
[31] A source book in mathematics, 1200–1800. Ed. by D.I.Struik Cambridge, Massachusets, 1969.
[32] Mugler Ch. Op. cit. P. 315, n. 1.
[33] A sourcebook in mathematics..., P. 81.
[34] Гоббс Т. Соч.: В 2 т. Т. 1. М., 1989. С. 74–75.
[35] Цит. соч. С. 76.
[36] Декарт Р. Цит. соч. С. 90.
[37] К.Бойер отмечает тот парадокс, что «метод Декарта есть метод координатной геометрии, но его цель мы отнесли бы в настоящее время скорее к теории уравнений, чем к аналитической геометрии» (Воуег C.B. History of Analytic Geometry, N.-Y., 1956. P. 101).
[38] Складывать и вычитать можно, вообще говоря, только однородные величины (что подчеркивал в своих трудах Виет). Но Декарт заметил, что умножением и делением на единицу длины можно всегда обеспечить эту однородность. Поэтому, например, в рассматриваемом примере можно считать х и р – имеющими размерность длины, q – размерность площади.
[39] Цейтен Г. История математики в XVI и XVII веках. М.; Л., 1933. С. 211.
[40] Декарт Р. Избранные произведения. М., 1950. С. 80 и далее.
[41] Не путать этого специального понимания интуиции с тем, которым мы пользовались (и будем пользоваться), характеризуя «теорийную» компоненту геометрии)
[42] Декарт Р. Избранные произведения. С. 89.
[43] Речь идет о теореме, например, такого вида: если a : b = c : d, то a : c = b : d.
[44] Аристотель. Вторая аналитика. 74а, 17–24.
[45] Подробнее см. в моей статье: Аналитическая геометрия Декарта и проблемы философии техники. Вопросы философии, 1989. № 12.
[46] Декарт Р. Геометрия. М.; Л., 1938. С. 31–32,74–75.
[47] Цит. соч. С. 30.
[48] Аналогичных взглядов держится и Лейбниц. Так он пишет Я.Томазию: «Но если мы рассмотрим дело ближе, то окажется, что геометрия доказывает именно из причин. В самом деле, она выясняет фигуры из движения: из движения точки происходит линия, из движения линии – поверхность, из движения поверхности – тело, из движения прямой по прямой происходит плоскость, иэ движения прямой вокруг неподвижной точки происходит круг и т.п. Таким образом, построение фигур есть движение; свойства же фигур, доказываются из построений, т.е. из движения, следовательно, априори и из причин. Значит, геометрия есть истинная наука». (Лейбниц Г.В. Соч.: В 4 т. Т. 1. С. 94).
[49] Proclus... Р. 47.
[50] Cossirer E. Leibuiz' System..., S. 4.
[51] Op. cit.S. 5.
[52] Op. cit. S. 6.
[53] Здесь прежде всего имеются в виду философские взгляды Николая из Кузы и его последователей.
[54] Ньютон И. Всеобщая арифметика или книга об арифметических синтезе и анализе. М., 1948. С. 298. См. подробнее об этой полемике в статье: Катасонов В.Н. Аналитическая геометрия Декарта и проблемы философии техники // Вопр. философии. 1989, № 12.
[55] Декарт Р. Геометрия... С. 14.
[56] Это хорошо знают преподаватели геометрии.
[57] Аналогично обстоит дело – и логически и исторически – с вопросом обоснования математической теории вероятностей. См. книгу: Катасонов В.Н.Метафизическая математика XVII века. М., 1993.
[58] Декарт Р. Цит. соч. Т. 1. С. 102.
[59] Там же. С. 103.
[60] Платон. Менон, 80 в.
[61] См., например: Менон. 76е-77.